У цьому розділі ми будемо обговорювати ті ж питання, що і в попередній, але з великими математичними подробицями. Якісно ми вже показали, що поле випромінювання двох джерел має максимуми і мінімуми, і тепер наше завдання - дати математичне, а не просто якісний опис поля.
Ми цілком задовільно розібрали фізичний зміст формули (28.6), розглянемо тепер деякі її математичні риси. Перш за все поле заряду, що рухається вгору і вниз з малою амплітудою в напрямку θ від осі руху, перпендикулярно променю зору і лежить в площині прискорення і променя зору (фіг. 29.1). Позначимо відстань через r, тоді в момент часу t величина електричного поля дорівнює
де a (t-r / c) - прискорення в момент часу (t-r / c), або запізнюється прискорення.
Цікаво намалювати картину розподілу поля в різних випадках. Найбільш характерний множник у формулі (29.1) - це a (t-r / c); щоб його зрозуміти, візьмемо найпростіший випадок θ = 90 ° і зобразимо поле на графіку. Раніше ми були зайняті питанням, як веде себе поле в даній фіксованій точці простору з плином часу. Тепер подивимося, як виглядає поле в різних точках простору в один і той же момент часу. Інакше кажучи, нам потрібен «моментальний знімок» поля, з якого буде ясно, як воно в різних місцях. Зрозуміло, картина розподілу поля залежить від прискорення заряду. Задамо характер руху заряду: нехай спочатку він спочиває, потім раптово почне певним чином прискорюватися (як показано на фіг. 29.2) і, нарешті, зупиниться. Потім, трохи пізніше, виміряємо поле в різних точках простору.
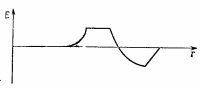Ми можемо стверджувати, що поле буде мати вигляд, наведений на фіг. 29.3. Справді, поле в кожній точці визначається прискоренням заряду в попередній момент часу, причому під словом «попередній» розуміється r / с секунд тому. Чим далі точка, тим більш раннім моментом часу визначається для неї прискорення. Тому крива на фіг. 29.3 в деякому сенсі є «звернений» в часі графік прискорення; час і відстань відрізняються постійним множником з який часто вибирається рівним одиниці. Цей факт легко помітити і в математичного запису a (t-r / c). Ясно, що добавка інтервалу часу Δt і віднімання відрізка шляху Δг = - c Δt дають одну і ту ж величину a (t-r / c).
Іншими словами, збільшивши час на Δt, можна відновити значення a (t-r / c) додаванням відрізка Δr = c Δt т. Е. Поле поширюється згодом як хвиля, що йде від джерела. Ось чому іноді говорять, що світло рухається як хвиля. Можна також сказати, що поле запізнюється в часі, або інакше, що поле поширюється вшир з плином часу.
Особливий інтерес представляє випадок періодичних коливань заряду q. Під час експерименту, розглянутому в гол. 28, зміщення зарядів х в момент t дорівнювало деякої константи х0, амплітуді коливань, помноженої на cos ωt. Прискорення в цьому випадку дорівнює
де a0, рівне -ω2xо, і є амплітуда прискорення. Підставляючи цю формулу в (29.1), знаходимо
Відвернемося поки від кута θ і постійних і подивимося, як веде себе Е (29.3) в залежності від часу або координат.
Соціальні коментарі Cackl e
