Д

Д.т.н., проф. Лежнюк П.Д., к.т.н., доц. Рубаненко О.Є.,

асп. Килимчук А.В.

Вінницький національний технічний університет

Оптимальне Управління нормальними режимами електроенергетичної системи з використанням крос-трансформаторів.

Паралельна робота ліній електропередач (ЛЕП) різної напруги через високу заходи неоднорідності викликає труднощі при транспортуванні і розподілі електроенергії. Між електричними мережами електроенергетичної системи (ЕЕС) через неоднорідність виникають взаємні потоки потужності, які завантажують мережі суміжних е нергоснабжающіх компаній. Відомо, що мережі високої напруги розвантажуються на паралельно працюючі мережі низької напруги. В результаті цього виникають додаткові втрати електроенергії, а також перевантаження комутаційних апаратів і ЛЕП низької напруги.

Дослідження заходи впливу взаємних і транзитних перетоків потужності на рівень втрат електроенергії є актуальним завданням. Її рішення дозволить контролювати і оцінювати вплив перетоків потужності магістральних електричних мереж на додаткові втрати в розподільних мережах обласних енергетичних компаній, а також аналізувати наслідки взаємовпливу електричних мереж. Компенсація додаткових втрат електроенергії в електричних мережах, викликаних їх взаємовпливом, можлива шляхом введення в контури е.р.с. лінійними регуляторами типу крос-трансформаторів (КТ) та силовими трансформаторами з РПН. Тобто робота розглянутих тут систем автоматичного управління (САУ) трансформаторами зв'язку ЕЕС, які об'єднують електричні мережі різних напруг в електричну систему, спрямована на зменшення втрат електроенергії при її транспортуванні в ЕЕС шляхом перерозподілу природних потоків потужності і примусового наближення їх до потокорозподілу в однорідній ЕЕС.

В роботі завдання оптимізації режимів ЕЕС ставиться як задача автоматичного управління, кінцевою метою розв'язання якої є формування закону оптимального управління режимами електричних мереж з урахуванням системного ефекту.

Закон оптимального керування нормальними режимами ЕЕС. Дослідження показали, що використання узагальнених методів теорії подібності дає можливість отримати в критеріальною формі аналітичні залежності між параметрами режимів [1]. Відповідно до поставленим завданням для формування законів управління САУ необхідно отримати критеріальні залежності між оптимальними керуючими впливами для вирішення задачі оптимізації токораспределения в ЕЕС в різних режимах її роботи. Як аргумент цільової функції доцільно прийняти зрівняльні е.р.с., які вводяться в контури ЕЕС з метою компенсації її неоднорідності.

Активні і реактивні складові зрівняльного х е.р.с. в критеріальною формі (за умови, що базисний режим є оптимальним зі значеннями Е (б) ур. а Σ, Е (б) у р.р Σ, J (б) а Σ, J (б) р Σ, записаними у вигляді діагональних матриць) 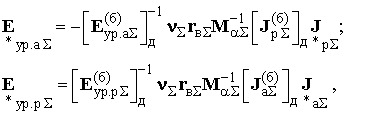(1):

(1)

де елементи векторів 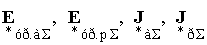визначаються як відношення відповідних параметрів поточного і базисного режимів.

У такій постановці завдання, які керують змінними є е.р.с., які необхідно ввести коефіцієнтами трансформації в усі замкнуті контура для реалізації оптимального токораспределения. В [2] показано, що оптимальне значення втрат в ЕЕС досягається при відносних значеннях е.р.с., які визначаються відповідно до формулами 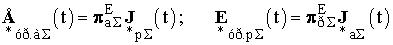(2):

, (2)

де 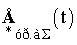, 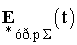- вектори активних і реактивних складових відносних значень зрівняльних е.р.с. трансформаторів з РПН і крос-трансформаторів, якими вводяться зрівняльні струми 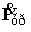; , 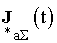- вектори активних і реактивних складових відносних значень струмів у вузлах; , 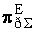- матриці критеріїв подібності.

Як бачимо, зрівняльні е.р.с. оптимальних режимів визначаються з урахуванням постійних коефіцієнтів (критеріїв подібності), що не залежать від параметрів поточного режиму. Вони подібні відповідним е.р.с. режиму, прийнятого за базисний. Тобто, в ЕЕС зрівняльні е.р.с. подібні для різних режимів. Для визначення оптимального режиму ЕЕС залишається ввести їх в контуру і виконати розрахунок усталеного режиму.

Матриці критеріїв подібності визначаються:

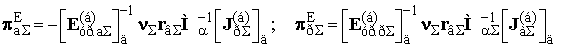, (3)

де 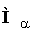- матриця з'єднань віток у вузлах дерева схеми.

Для автоматичної реалізації оптимальних коефіцієнтів трансформації необхідно отримати відповідні закони управління. Це завдання зводиться до задачі формування прийнятих на початку розрахункових умов і може бути вирішена як описано в [3].

З усіх трансформаторів з РПН, в ЕЕС для управління втратами потужності відбираються (в результаті критериального аналізу) кілька (q) таких крос-трансформаторів, які мають найбільший регулювальний ефект [1]. Якщо тепер розрахункову модель ЕЕС сформувати таким чином, що всі q трансформаторів будуть знаходитися в хордах базисної системи контурів, то їх коефіцієнти трансформації дорівнюватимуть:

.

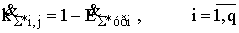Тоді вектор оптимальних коефіцієнтів трансформації запишеться:

або

,

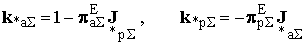де k * аΣ, k * рΣ - вектори дійсних і уявних складових коефіцієнтів трансформації в відносних одиницях.

Останній вираз коефіцієнтів трансформації для системи автоматичного управління є законом оптимального керування нормальними режимами ЕЕС. З урахуванням фактору часу вони записуються в такому вигляді 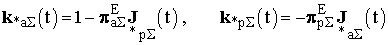(4):

. (4)

Кінцеві розрахункові формули законів оптимального управління трансформаторами з РПН і з крос-трансформаторами з урахуванням приведення параметрів ЕЕС до напруги базисного вузла мають вигляд 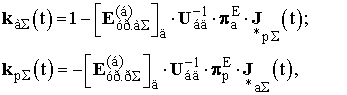(5):

(5)

де U бд - діагональна матриця, кожен елемент якої дорівнює напрузі базисного вузла.

Ці закони є основою функціонування CАУ [5]. Як видно з (5) вони визначаються неоднорідністю і заходом незбалансованості коефіцієнтів трансформації трансформаторного обладнання ЕЕС. Їх реалізація компенсує, з точністю до ступеня регулювання коефіцієнтів трансформації, неоптимальність потокораспределения в ЕЕС, яка викликана неоднорідністю і наближає втрати потужності в ЕЕС до мінімальних.

Як видно з (5), математичний опис законів функціонування САУ, регульованими трансформаторами, є досить складним, а їх формування, адаптація і реалізація, вимагають істотних витрат машинного часу, особливо, з огляду на необхідність корекції матриці критеріїв подібності в разі істотних змін стану регулювальних пристроїв. Необхідні обчислення втрат і обсяги передачі інформації можуть бути істотно знижені, якщо на етапі математичного моделювання врахувати умови практичної реалізації розроблених моделей.

Математична модель оптимального управління усталеного режиму ЕЕС

Таким чином, отримана математична модель оптимального управління усталеного режиму ЕЕС, в тимчасовій області, у вигляді линеаризованной багатовимірної системи із зосередженими постійними параметрами.

Е.р.с. в контури вводяться зі спільною роботою трансформаторів з РПН і КТ. За допомогою КТ вводиться базова частина змінної в часі Е * ур е.р.с. Е * кт, до якої ступенями Δ E * АТ додається е.р.с. трансформаторів з РПН. З урахуванням зв'язку між контурними е.р.с. і коефіцієнтами трансформації трансформаторів, за певних умов (трансформатори в базовій системі контурів знаходяться в хордах, кількість регульованих трансформаторів дорівнює кількості контурів), коефіцієнти трансформації КТ і трансформаторів з РПН можуть бути переписані у вигляді [6]:

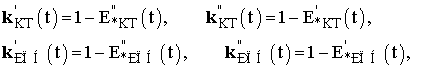
де 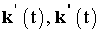- вектори дійсних і уявних складових коефіцієнтів трансформації відповідно трансформаторів з РПН і КТ.

Висновки: розроблена математична модель зрівняльних е.р.с. в електричних системах, яка на відміну від існуючих, містить коефіцієнти трансформації крос-трансформаторів і трансформаторів з РПН, що дає можливість враховувати вплив крос-трансформаторів на у равнітельние струми з метою зменшення незбалансованих коефіцієнтів трансформації, неоднорідності ЕЕС і наслідки їх взаємовпливу. Показано, що отримані критеріальні залежності є законами оптимального управління. При певних умовах вони змінюються з урахуванням параметрів крос-трансформаторів і можуть бути використані в якості законів управління адаптивних САУ нормальними режимами ЕЕС.

література

1. Лежнюк Петро Дем 'янович, Автоматизація керування потоками потужності та напругою в електричних системах на основе Теорії подібності /П.Д. Лежнюк, К.І. Кравцов, С.Я. Вишневський // Управління енерговікорістанням: Збірник доповідей / Під ред. А.В. Праховніка. - К .: Альянс за Збереження ЕНЕРГІЇ, 2001. - С. 219-224.

2. Автоматизація управління енергооб'єднаннями / Гончуков В.В., Горнштейн В.М., Крумм Л.А. та ін. - М .: Енергія, 1979.- 432 с.

3. Petro Lezhnukm. Optimal control of power flows in electric power systems using theory of similarity / Petro Lezhnuk, Eugene Didichenko, Konstantin Kravtsov // Proceedings of the 5th International Conference on "Development and application systems" (DAS - 2000). - Suceava, Romania: "MUSATINII", 2000. - С. 10-15.

4. Лежнюк Петро Де 'м Янові ч. Натурно - імітаційне моделювання з Використання критеріального методу в оптимальному керуванні електроненергетічнімі системами / П. Д. Лежнюк, В.М. Гайдамака // Вісник Вінницького політехнічного інституту. - 2003. - № 1. - С. 37-41.

5. Автоматизація керування потоками потужності в ЕЕС з Використання крос - трансформаторів та подібності оптимальних режімів [Електронний ресурс] / П. Д. Лежнюк, Жан - П 'єр Нгома, А. В. Килимчук // Вінницький національний технічний університет - 2009. - №4 - режим доступу до журн. http://www.nbuv.gov.ua/e-journals/vntu/2009-4/2009-4_ru.files/ru/09pdloms_ru.pdf