ТЕРМОДИНАМІКА

1. ЕНЕРГІЯ
2. Механічний еквівалент теплоти.
3. Робота.
4. «Корисність» енергії.
5. Перший початок термодинаміки.
6. Другий закон термодинаміки.
7. Третій закон термодинаміки.
8. ТЕПЛОВІ МАШИНИ
9. Цикл холодильної машини.
10. Інші цикли теплової машини.
11. ТЕРМОДИНАМІЧНІ ФУНКЦІЇ
12. Ентропія.
13. Ентальпія.
14. Вільна енергія.
15. Потенціал Гіббса.
16. Співвідношення між термодинамічними функціями.
17. Теплоємність.
18. Обчислення ентропії.
19. Невпорядкованість і ентропія.
20. Рівновага.
21. Термодинамічні співвідношення.
22. Застосування співвідношень Максвелла.
23. Вплив тиску.
24. Ефект Джоуля - Томсона.
25. Вплив температури.
26. Інші співвідношення.
27. Рівняння стану.

ТЕРМОДИНАМІКА, розділ прикладної фізики або теоретичної теплотехніки, в якому досліджується перетворення руху в теплоту і навпаки. У термодинаміки розглядаються не тільки питання поширення теплоти, але і фізичні і хімічні зміни, пов'язані з поглинанням теплоти речовиною, а також, навпаки, виділення теплоти в ході фізичних і хімічних перетворень.

Термодинаміка знаходить широке застосування у фізичній хімії та хімічної фізики при аналізі фізичних і хімічних процесів, в сучасній фізіології і біології, в двигунобудування, теплотехніки, авіаційної і ракетно-космічної техніки. Спочатку в термодинаміки багато уваги приділялося оборотних процесів і рівноважним станам, так що більш відповідним для неї здавалося назву «термостатики», але завдяки С.Арреніус (1859-1927) і Г.Ейрінгу (1901-1981) отримало вельми ґрунтовну розробку її застосування до аналізу швидкостей хімічних реакцій (хімічної кінетики). В даний час головною проблемою в термодинаміки є її застосування до незворотних процесів, і вже досягнуті великі успіхи в побудові теорії, за широтою охоплення порівнянної з термодинамікою оборотних процесів.

ЕНЕРГІЯ

Для тієї фізичної величини, яку ми тепер називаємо енергією, довгий час вживався термін «жива сила», введений И.Ньютоном (1643-1727). Але оскільки «живу силу» можна було сплутати зі звичайною силою, останню доводилося для ясності називати «мертвої силою», що не можна визнати вдалим. Спеціальний термін «енергія» був введений в 1807 Т.Юнгом (1773-1829).

Одним з видів енергії є робота, яка відбувається, коли тіло рухається, долаючи дію якоїсь сили. Прикладом може служити подача насосом води в водонапірну вежу. Про воду в башті кажуть, що вона має потенційну енергію. Завдяки гравітаційному тяжінню Землі існує можливість зворотного перетворення цієї енергії в кінетичну, тобто в енергію руху води, що тече по трубах. Коли вода в трубі в кінці кінців зупиняється через внутрішнього тертя, або в'язкості, ця енергія виявляється перетворилася в теплоту, тобто теплову енергію, яка розсіюється в навколишньому середовищі.

Ще в 1620 Ф. Бекон висловив припущення, що теплота є просто інша форма руху, але лише в 1789 це з переконливістю встановив Б.Томпсон (Румфорд), спостерігаючи за виділенням теплоти при розсвердлюванні стовбура гармати. Додатковим підтвердженням з'явилися досліди Х.Деві 1799.

Ці досліди і спостереження говорили про те, що теплова і механічна енергія - одне і те ж і що, ймовірно, можна знайти експериментально механічний еквівалент теплоти, тобто кількість роботи в механічних одиницях, еквівалентну даному кількості теплоти в теплових одиницях.

Механічний еквівалент теплоти.

Помітивши, що температура води в медичній колбі підвищується, якщо її кілька хвилин струшувати, Ю.Майер в 1842 обчислив механічний еквівалент теплоти по різниці питомих теплоємностей повітря при постійному тиску і постійному обсязі. В ту пору точні значення цих питомі теплоємності ще не були відомі, а тому його результат був не зовсім вірним, хоча і правильним по порядку величини. У 1845 Дж.Джоуль точно виміряв кількість теплоти, що отримується при перетворенні механічної роботи в теплову енергію, і уточнив результат Майера.

Робота.

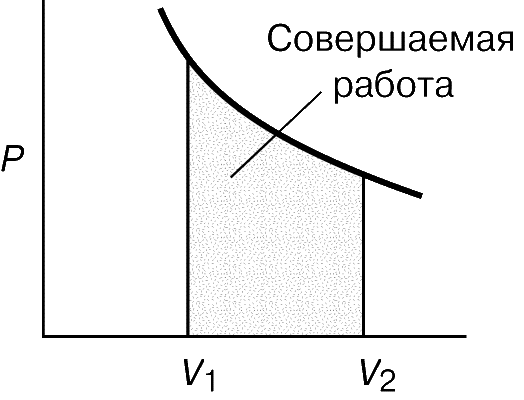
Якщо якась речовина знаходиться під обмежуючим впливом зовнішньої сили, наприклад атмосферного тиску P, то при зміні його об'єму V, скажімо розширенні, внаслідок руху проти чинної сили відбувається робота. Повну здійснюються роботу можна знайти як площа залежності сили від відповідного розміру, як показано на рис. 1, де площею ділянки, виділеного ретушшю, представлена робота, що здійснюються газом при розширенні від V 1 до V 2. Такий спосіб її визначення необхідний, оскільки тиск може змінюватися. При малій зміні обсягу тиск набагато не зміниться, так що мала кількість яку здійснюють роботи дорівнюватиме:

Отже, повна здійснюються робота

При швидкому стискуванні газу деяка частина роботи, яку здійснюють над ним, може помітно підвищити його температуру. Якщо газ знаходиться в теплоизолированном посудині (або стискається настільки швидко, що не встигає хоча б частково віддати свою теплоту), така зміна обсягу називається адіабатичним. Якщо ж газ не теплоізольований, то відбувається тепловіддача, і газ зберігає температуру навколишнього середовища. Така зміна обсягу називається ізотермічним.

«Корисність» енергії.

Повне перетворення роботи в теплоту цілком можливо, але зворотний процес перетворення всієї теплоти в еквівалентну їй роботу неможливий. До такого висновку ще в 1824 прийшов шляхом теоретичних міркувань французький фізик Н.Карно (1796-1832). Розглядаючи повний цикл оборотних змін робочого тіла в тепловій машині, в кінці якого це тіло повертається в початковий стан, він показав, що максимальний ККД перетворення теплоти в роботу залежить не від природи робочого тіла, а тільки від максимальної температури, при якій підводиться теплота, і від мінімальної температури, при якій вона відводиться. Повне перетворення теплоти в роботу було б можливо лише в тому випадку, якщо б мінімальна температура була дорівнює абсолютному нулю, при якій робоче тіло не мало б ніякої теплової енергії.

На існування абсолютного нуля вказує закон розширення газів. Оскільки при охолодженні від 0 до - 1 ° C гази стискаються на 1/273, можна уявити собі якийсь «ідеальний» газ, який не конденсується, як реальні гази, але з пониженням температури продовжує стискатися, поки його об'єм не зменшиться до нуля при - 273 ° C. Це було б абсолютним нулем температури для теплової машини, робочим тілом якої є ідеальний газ. Провівши набагато більш складні міркування, У.Томсон (Кельвін) (1824-1907) довів, що це дійсно абсолютний нуль температури, і ввів названу його ім'ям «термодинамічну» шкалу температури T (шкалу Кельвіна), відповідно до якої T = 273, 16 + t ° C.

Перший початок термодинаміки.

для В.Лейбніца (1646-1716) було вже незаперечним, що в консервативній системі (подібної гравітаційного поля) сума кінетичної і потенційної енергій залишається незмінною, які б перетворення однієї в іншу не відбувалися. Простий приклад - маятник, кінетична енергія якого періодично переходить в потенційну і назад, причому це могло б тривати до нескінченності, якби енергія не розсіюється через тертя. Однак є тертя в підвісі, а також опір повітря, теж обумовлене тертям. Тому маятник в кінці кінців втрачає кінетичну енергію свого видимого руху, але досліди Румфорда і інших вчених свідчили про те, що енергія лише перетворюється в теплоту, і в результаті цього підвищується температура маятника і навколишнього середовища. Таким чином, строго періодичні коливання маятника перетворюються в хаотичний рух його молекул і молекул навколишнього середовища.

Все викладене знаходить загальне вираження в першому початку термодинаміки - закон збереження енергії. Згідно з цим законом, у всіх таких перетвореннях енергія не виникає і не зникає, вона лише змінює форму. На це вказав в 1837 чудовий, але майже невідомий мислитель К.Мор в своїй статті Про природу теплоти (On the Nature of Heat): «При відповідних умовах енергія може проявлятися як рух, злипання, електрику, світло, теплота і магнетизм». Закон збереження енергії був чітко сформульований в 1847 Г.Гельмгольц (1821-1894), але і після цього універсальний характер закону не відразу отримав визнання. У 20 ст. його довелося ще більш узагальнити, включивши в нього теоретично встановлене А.Ейнштейном співвідношення E = mc 2 між масою m і енергією E (c - швидкість світла), з якого випливає, що сума маси і енергії залишається незмінною.

Другий закон термодинаміки.

Хоча повна енергія ізольованої системи залишається постійною, теплота передається від нагрітої частини системи до більш холодної, і, якщо ці частини не ізольовані один від одного, їх температура в кінці кінців стає однаковою. Дане положення, відоме нам з досвіду повсякденного життя, іноді називають «нульовим» початком термодинаміки.

В результаті такого вирівнювання внутрішніх температур ізольована система переходить в своє найбільш ймовірне стан, в якому рух гранично хаотично. Таке мимовільне прагнення до стану з найвищим ступенем хаотичності є, інакше кажучи, прагнення до максимальної ентропії, яку можна розглядати як міру «марності» енергії в термодинамічній системі. Суть другого закону термодинаміки, сформульованого в 1850 Р.Клаузиус (1822-1888), і полягає в тому, що в ізольованій системі внутрішній розподіл енергії мимовільно завжди змінюється так, що ентропія досягає максимального значення ціною зменшення корисної частини енергії. В силу цього неможливий вічний двигун другого роду (перпетуум-мобіле II).

Необоротне наростання ентропії в теплових процесах незрозуміло тим, хто тільки почав знайомитися з термодинаміки, але його неважко пояснити, спираючись на теорію ймовірностей. Уявімо собі дві гральні кістки, що лежать вгору шістками. Якщо ми потряс їх, перш ніж знову викинути, то ймовірність випадання двох шісток буде мала - 1:36. Таким чином, можна сказати, що безладний рух (перемішування) гральних кісток, подібно хаотичного руху молекул, відповідному їх теплової енергії, виявляється причиною переходу з менш ймовірного стану в більш ймовірне. Якщо ж у нас мільйони гральних кісток (атомів і молекул, для яких проводяться термодинамічні розрахунки), то ймовірність одночасного випадання всіх шісток ця величина настільки мала, що система просто не може не перейти в один з найбільш ймовірних станів.

Якщо теплота - безладне коливальний рух молекул, то при охолодженні ентропія системи повинна зменшуватися. Коли ж тепловий рух повністю припиниться, система буде при абсолютному нулі температури. Природно припустити, що при такій температурі ентропія дорівнює нулю.

Третій закон термодинаміки.

Щоб знайти абсолютне значення ентропії, необхідно знати теплоємність при абсолютному нулі температури. Вимірявши теплоємність багатьох речовин при температурах, дуже близьких до абсолютного нуля, В.Нернст (1864-1941) прийшов до висновку, що теплоємність всіх кристалічних речовин при абсолютному нулі температури дорівнює нулю. Ця «теплова теорема Нернста» тепер називається третім початком термодинаміки. Її значення в тому, що вона дозволяє порівнювати між собою ентропії різних речовин, так як всі вони дорівнюють нулю при абсолютному нулі температури.

ТЕПЛОВІ МАШИНИ

Цикл Карно.

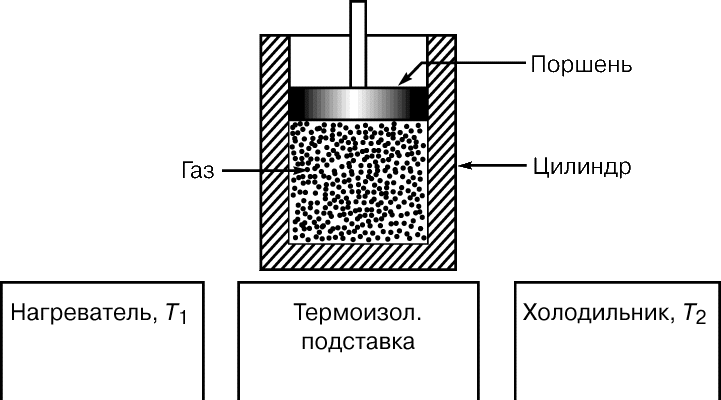
До 1824 коли Карно опублікував свій трактат Роздуми про рушійну силу вогню ... (Réflections sur la puissance motrice du feu ...), було вже добре відомо, що за рахунок теплоти можна одержувати механічну енергію, але ні в кого не було ні найменшого уявлення про те, яким може бути ККД теплової машини, і були не зовсім зрозумілі термодинамічні основи її дії. Минуло десять років, перш ніж Б.Клапейрон, який першим по достоїнству оцінив трактат Карно, повторно опублікував його, забезпечивши важливими доповненнями. Карно представляв теплову машину (рис. 2) у вигляді ідеально теплоізольованої циліндра, наповненого фіксованою кількістю робочого тіла (газу) і забезпеченого що рухається без тертя поршнем. Машину можна без енергетичних втрат переносити з одного підставки на іншу. Одна підставка, підтримувана при температурі T 1, служить нагрівачем. Іншу, підтримувану при більш низькій температурі T 2, назвемо холодильником. Спочатку циліндр стоїть на нагрівачі, і газоподібне робоче тіло ізотермічні (тобто поглинаючи теплоту так, що його температура не змінюється) розширюється від точки 1 до точки 2 на графіку залежності об'єм - тиск (рис. 3, а). Потім машину переносять на теплоизолированную підставку і газ адіабатичні розширюється від точки 2 до точки 3, здійснюючи роботу - піднімаючи поршень. В результаті він охолоджується до температури T 2. Після цього машину переставляють на холодильник, і газ ізотермічні стискається від точки 3 до точки 4, віддаючи теплоту холодильнику. Переставивши потім машину знову на теплоизолированную підставку, можна тепер адіабатичні стиснути газ від точки 4 до точки 1 і повернути його в початковий стан (до колишніх значень температури, обсягу і тиску), так що цикл може початися знову.

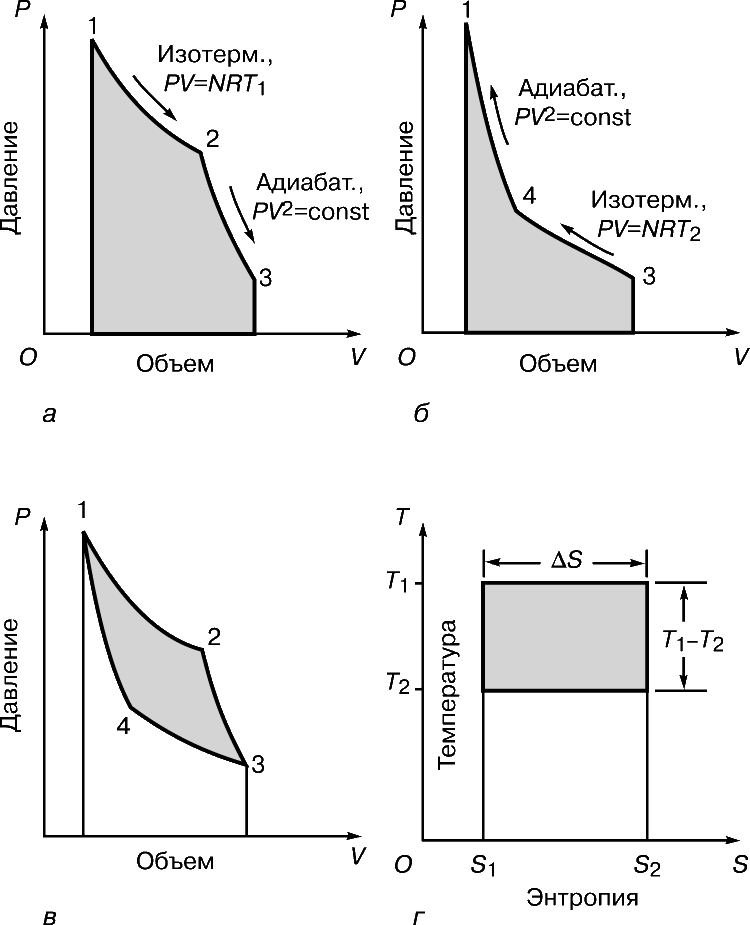
Мірою корисної роботи, досконалою машиною, є різниця площ (рис. 3, а і б), показана на рис. 3, ст. Неважко здогадатися, що при заданій зміні обсягу цю різницю площ можна збільшити або підвищивши T 1, або знизивши T 2. Якщо ж температура T 1 фіксована (а це значить, що фіксоване повну кількість підводиться теплоти), то роботу, вироблену машиною, можна збільшити , тільки знизивши T 2. З особливою наочністю це показує «діаграма Молье» (графік залежності температура - ентропія), представлена на рис. 3, м. Тут теж корисна робота пропорційна виділеної площі; підводиться теплота визначається площею T 1 D S, а частина її, відповідна площі прямокутника T 2 D S, «марна» в сенсі здійснення роботи. Таким чином, як і вона була температура T 1, відмінна від абсолютного нуля, якась частина підводиться теплоти не може бути перетворена в роботу.

На викладених міркуваннях заснований висновок формули Карно, яка дає максимально можливий ККД ідеальної теплової машини, що працює при заданій різниці температур нагрівача і холодильника:

Реальна машина не може працювати з таким ККД, оскільки в ній неминучі тертя і витоку тепла. Для парової машини, що працює, наприклад, при температурі котла 130 ° C (403 К) і температурі конденсатора 30 ° C (303 К), термодинамічний ККД дорівнює 100/403, тобто менше 25%.

Цикл холодильної машини.

Оскільки робоче тіло в циклі Карно повертається в початковий стан, можна уявити собі звернену теплову машину. Якщо в прямому циклі передача тепла від нагрівача до холодильника використовується для отримання роботи, то в зверненому за рахунок здійснення механічної роботи теплота передається від холодильника нагрівача, так що холодильник стає ще холодніше, а нагрівач - ще гаряче. Такий цикл холодильної машини (використовуваний, наприклад, в холодильниках і кондиціонерах): робота, що здійснюються електродвигуном домашнього холодильника, йде на те, щоб усередині холодильника було холодно за рахунок нагрівання навколишнього повітря.

Інші цикли теплової машини.

У реальних теплових машинах цикли з ізотермічними процесами не знаходять застосування, оскільки такі процеси вимагають багато часу. Перевага віддається адиабатическим процесам, бо вони ближче до реальності в швидко працюють машинах. Найпростіший з таких циклів - цикл Отто (рис. 4, а), названий по імені німецького винахідника та інженера Н.Отто (1832-1891). У цьому циклі підводиться теплота підвищує тиск газу при постійному обсязі, а потім газ адіабатично розширюється з вчиненням корисної роботи. Після того як досягнуто заданий обсяг, теплота відводиться, а частина роботи витрачається на адіабатичне стиснення газу, після чого цикл може повторитися. ККД визначається ступенем стиснення r:

де g - відношення питомих теплоємностей газу при постійному тиску і при постійному обсязі. Чим більше r, тим більше ККД.

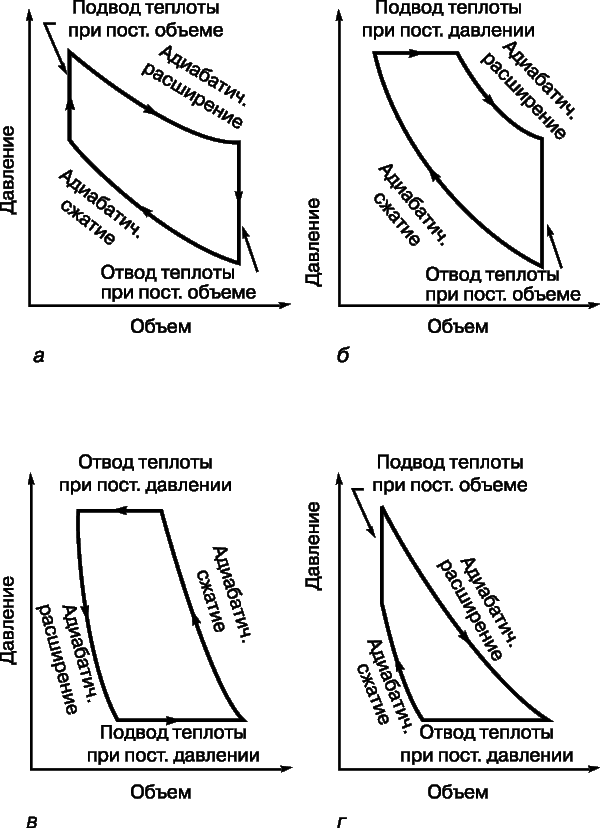
Цикл Дизеля (рис. 4, б) названий по імені німецького винахідника Р. Дизеля (1858-1913). У цьому циклі теплота теж віддається при постійному обсязі після адіабатичного розширення, але підводиться (після адіабатичного стиснення) при постійному тиску. У дизельному двигуні тепло не підводиться від зовнішнього джерела, а виробляється всередині при згорянні палива, самовоспламеняющегося при сильному стисненні. Високотемпературні гази не охолоджуються, а роблять роботу і виводяться назовні з заміною холодної сумішшю палива з повітрям. Теоретичний цикл майже повністю відтворюється, якщо не брати до уваги впливу механічних факторів і інших неминучих теплових втрат.

У менш відомому циклі Аткінсона (рис. 4, г) послідовність гілок обратна послідовності в циклі Дизеля. Тільки в циклі Джоуля (рис. 4, в) теплота і віддається і підводиться при постійному тиску, але цей цикл зазвичай не використовується для перетворення теплоти в роботу; він застосовується в зверненої (холодильної) машині.

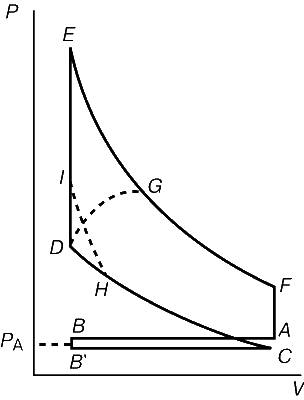
Графіки залежності Тиск - ОБСЯГИ типу представлених на рис. 3 і 4 назіваються індікаторнімі діаграмамі. Ними корістуються Інженери для розрахунку ККД двигунів. Для прикладу на рис. 5 представлена ​​індікаторна Діаграма чотірітактного бензинового двигуна. За тактом стиснення CD, що починається в точці C, слідують згоряння палива на вертикальній гілки DE і робочий такт EF. У точці F відкривається випускний клапан, так що тиск знижується до атмосферного тиску PA, і відпрацьовані гази викидаються з циліндра двигуна відповідно горизонтальної гілки AB. На ділянці B ў C в циліндр впускается нова горюча суміш, і цикл закінчується. У реальному двигуні згоряння не відбувається миттєво. Якщо запалювання виробляється в точці D, то полум'я поширюється по циліндру, коли обсяг уже почав збільшуватися, і тому максимальне теоретичне тиск не досягається. Значна частина площі, пропорційної яку здійснюють роботі, втрачається, що показано штриховою лінією DG. Якщо ж запалення проводиться з випередженням, наприклад в точці H, то втрачається лише мала частина корисної площі, як показано штриховою лінією HI. Це пояснюється тим, що при наростанні тиску обсяг все ще продовжує зменшуватися.

ТЕРМОДИНАМІЧНІ ФУНКЦІЇ

Внутрішня енергія.

Коли до системи підводиться деяку кількість теплоти dQ, за рахунок цієї теплоти, як було показано раніше на прикладі циклу Карно, може бути здійснена лише певна робота dW, так що частина отриманої теплової енергії система втрачає. Ці дві величини, взагалі кажучи, неоднакові, і, отже, система або втрачає, або набуває енергію, рівну їх різниці. Припустимо, що ця різниця енергій залишається в системі у вигляді т.зв. внутрішньої енергії E. Тоді остання збільшиться від E до (E + dE), причому

де dQ і dW - нескінченно малі збільшення.

Взагалі кажучи, збільшення dQ і dW не є незалежними (чому вони і позначені тут символом d на відміну від збільшення dE). Так, поглинання теплоти зазвичай супроводжується зміною обсягу і, отже, вчиненням роботи проти зовнішнього тиску. І навпаки, якщо допускається розширення, то воно зазвичай супроводжується поглинанням теплоти, що відбирається у довкілля. Ніякі обмеження, що накладаються реально на систему, не можуть повністю виключити такої взаємодії, але подумки можна уявити собі ідеальну теплоізоляцію (d Q = 0) або строго що виконується умова постійного обсягу (d W = 0), так само як в теоретичній механіці вводяться поняття ідеально гладких і ідеально твердих тіл. Тільки в ідеальних умовах, коли dQ і dW незалежні один від одного, приріст dQ або dW можна розглядати як повний диференціал, тоді як їх різниця dE завжди є такою.

Ентропія.

Теплова енергія dQ ў, яка не може бути перетворена в роботу, пропорційна нижньої температурі T, так що можна записати dQ ў = TdS, де dS - приріст ентропії S системи. Як і E, величина S є характеристикою самої системи, а тому ми позначаємо її приріст буквою d, а не d.

Позначивши через dW роботу, яку можна отримати за рахунок теплоти dQ, можна написати

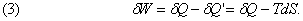
Якщо робоче тіло в результаті якогось термодинамічної процесу не повертається в початковий стан, то значна частина енергії не буде корисною з точки зору здійснення роботи, і внутрішня енергія збільшується на відповідну різницю dE. Збільшення внутрішньої енергії може проявитися в зміні фізичного стану робочого тіла, наприклад в переході з твердого в рідкий стан (плавленні) або з рідкого в газоподібний (випаровуванні). Така теплова енергія називається теплотою плавлення і теплотою пароутворення відповідно. Підвищення внутрішньої енергії може бути пов'язано також з хімічними змінами (дисоціацією, розривом зв'язків) і навіть з розподілом ядер.

Ентальпія.

Якщо зміни енергії системи відбуваються при постійному тиску, то, як виявляється, функція

дозволяє надати більш просту і витончену форму рівнянь, що описує різні процеси. Справа в тому, що при невеликій зміні стану системи в силу рівності (1) і (2) можна записати

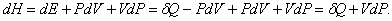
Отже, якщо процес протікає при постійному тиску (dP = 0), то виконується рівність

dH = dQ,

тобто підведене кількість теплоти може бути представлено у вигляді повного диференціала деякої величини, що характеризує внутрішній стан системи. Ця величина називається ентальпії. Раніше вона називалася теплової функцією або теплосодержанием системи.

Вільна енергія.

В ізотермічних умовах (dT = 0) більш, ніж H, зручна інша термодинамічна функція:

Такі ж викладки, як і в разі ентальпії, дають dF = d W. Раніше величина F називалася вільною енергією Гельмгольца, оскільки саме Гельмгольц першим вказав на її значення, але зараз її називають просто вільною енергією.

Потенціал Гіббса.

У тих випадках, коли змінюватися можуть і температура і тиск, використовується більш загальна функція

Цю функцію іноді називають повним термодинамічних потенціалом або корисної енергією, але зараз її прийнято називати потенціалом Гіббса або гиббсової енергією і позначати символом G по імені Дж.Гіббсом (1839-1903). Як буде показано нижче, представлені термодинамічні функції дозволяють визначити умови, необхідні для рівноваги.

У разі підвищення тиску на малу величину dP в системі, яку підтримує при постійній температурі (dT = 0), потенціал Гіббса збільшиться на величину dG, а швидкість його збільшення, або «чутливість» потенціалу Гіббса G до змін тиску, дається термодинамічних виразом для обсягу системи

де символ приватної похідної вказує на те, що зміна відбувається при постійних значеннях всіх інших параметрів (в даному випадку температури T).

Точно так же чутливість потенціалу Гіббса до змін температури (при постійному тиску) є міра ентропії системи:

і це рівність можна розглядати як ще одну постанову ентропії.

Співвідношення між термодинамічними функціями.

Величини E, H, F і G мають розмірність енергії, і будь-які три з них можуть бути виражені через четверту. Якщо dW = PdV, то, користуючись рівністю (7) і (8), можна H, F і E висловити через G:

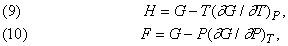
а отже,

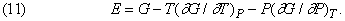
Якщо вважати функцією тільки G, то з незалежних змінних досить буде розглядати лише P і T, що майже завжди виявляється найбільш зручним. Якщо ж в якості єдиної функції вибрати E, то найзручнішими з математичної точки зору будуть незалежні змінні V і T або V і S, але остання з них, очевидно, не дуже зручна для прямих вимірювань.

Теплоємність.

Зміна ентропії dS речовини можна обчислити за кількістю теплоти, необхідного для підвищення його температури на один градус, тобто по виміряної теплоємності C. Але теплоємність залежить від того, чи може речовина розширюватися при постійному тиску P, так як тоді за рахунок теплоти повинна відбуватися робота, пов'язана з розширенням. Тому теплоємність при постійному тиску CP більше теплоємності при постійному обсязі CV. Ці величини даються равенствами

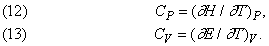
Різниця теплоемкостей CP і CV виражається в теплових одиницях, а надлишкова енергія, необхідна для здійснення роботи при розширенні проти сил тиску, може бути виражена у механічних одиницях [см. формулу (2) і рис. 1]. Саме так Майер і обчислив механічний еквівалент теплоти.

Обчислення ентропії.

Якщо тиск P постійно, то, оскільки H = E + PV, з урахуванням рівності (3) можна написати

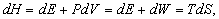
звідки

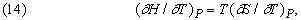
або

Отже, побудувавши графік залежності відношення CP / T від T (або, що з математичної точки зору те ж саме, графік залежності CP від ln T), можна знайти приріст ентропії D S як площа кривої на графіку (рис. 6):

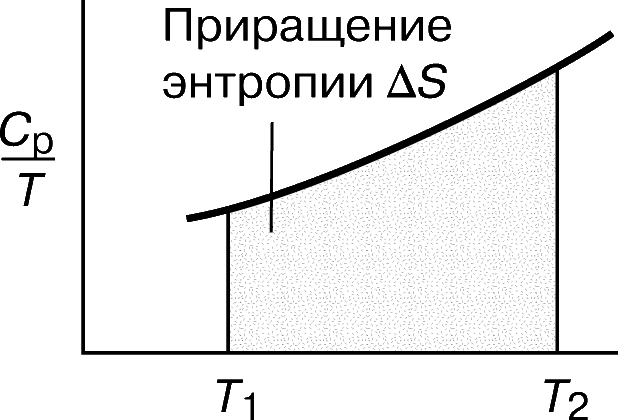
Невпорядкованість і ентропія.

Австрійський фізик Л.Больцман показав, спираючись на статистичну механіку, що ентропія є міра невпорядкованості, а саме:

де S - ентропія N молей речовини, а R - постійна із загального рівняння для газів

яке являє собою математичний запис окремих законів, відкритих Р. Бойл (1627-1691) і Е.Маріоттом (1620-1684) і об'єднаних Ж.Гей-Люссаком (1778-1850) з законом, встановленим Ж.Шарлем (1746-1823) . Універсальна газова стала R для всіх газів дорівнює 8,3144 Дж / моль Ч К.

Величина F - це число способів, якими енергія може бути розподілена серед молекул при даній температурі, віднесене до відповідного числа способів при абсолютному нулі температури. Якщо температура вище абсолютного нуля, то система прагне перейти в стан, в якому величина Ф більше, так як в цьому випадку буде менше енергія, яка припадає на кожну молекулу, а це більш ймовірна ситуація, ніж розподіл, при якому вся енергія припадає на невелике число молекул.

Таким чином, ентропія речовини, що знаходиться в даному стані, є відносна ймовірність цього стану, взята в логарифмічному масштабі і помножена на NR, для того щоб вона виражалася в термодинамічних одиницях.

Ідеальний кристал зі строго впорядкованим розташуванням всіх атомів - дуже малоймовірна структура, яка може підтримуватися лише при наявності великих міжатомних сил або, інакше кажучи, при низькому рівні його внутрішньої енергії. При нагріванні кристала тепловий рух порушує цю впорядкованість. При певній температурі (точці плавлення), коли теплова енергія стає більше енергії міжатомної взаємодії, тверда кристалічна решітка руйнується і речовина переходить в менш впорядковане рідкий стан. Вільна енергія, якої характеризується рівноважний стан [формула (5)], визначається співвідношенням між впорядкує дією внутрішньої енергії і разупорядочівающім дією підвищеної температури, причому ентропія служить кількісною мірою дії температури.

Рівновага.

Таким чином, умовою рівноваги при постійній внутрішній енергії є максимум ентропії S. Можливі деякі флуктуації, короткочасно виводять систему з цього стану, але в середньому за будь-досить тривалий час виконується рівність

dS = 0.

Оскільки величини F і G є функціями ентропії S, взятої зі знаком «мінус», дана умова означає, що рівновага можливо тільки тоді, коли або величина F, або величина G має мінімум. Таким чином, при будь-якому мислимому зміні dX умови рівноваги такі:

або

аналогічно

або

Зміна dX може являти собою збільшення обсягу, зменшення площі поверхні, скорочення довжини, збільшення електричного заряду, зменшення намагніченості або збільшення числа молекул. Енергетична функція тоді повинна мати ще більш загальну форму, ніж потенціал Гіббса G, а для того, щоб рівновагу було стійким, всі інші змінні - внутрішня енергія, ентропія, температура, тиск, поверхневий натяг, електричний потенціал, напруженість магнітного поля, хімічний потенціал - повинні змінюватися в строгому згоді з рівнянням (20). Така узагальнена формулювання принципу динамічної рівноваги, встановленого в 1884 французьким хіміком А.Ле Шательє (1850-1936). Введений ним принцип говорить: «Якщо на систему, що знаходиться в стійкому рівновазі, виявляється зовнішній вплив, то в системі відбувається таке зміщення рівноваги, яке послаблює цей вплив».

Термодинамічні співвідношення.

Диференціюючи рівняння, що зв'язують термодинамічні функції між собою, і залучаючи інші фундаментальні закони, можна вивести деякі важливі співвідношення між такими функціями.

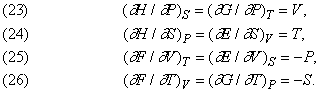
Рівняння (23) - (25) краще прояснюють фізичний зміст функцій E, H, F і G в їх зв'язку з більш звичними змінними V, T і P. Рівняння ж (26), як уже говорилося, дає ще одну інтерпретацію ентропії S з використанням функції F або G.

Дж.Максвелла (1831-1879) вивів наступні важливі співвідношення між змінними V, T, P і S:

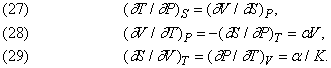
Тут a - коефіцієнт теплового розширення, віднесений до одиниці об'єму при постійному тиску, тобто (1 / V) (¶ V / ¶ Т) P, а K - ізотермічна стисливість - (1 / V) (¶ V / ¶ P) T.

Застосування співвідношень Максвелла.

Зі співвідношень Максвелла можна вивести інші цікаві співвідношення. Наприклад, можна обчислити теплоту пароутворення L деякої рідини, щоб з'ясувати, як вона залежить від зміни обсягу при випаровуванні. У першій частині подвійного рівності (29) величину ¶ S можна прирівняти L / T. Зміна обсягу dV дорівнює різниці (V- v) обсягу пара V і об'єму рідини v при температурі T, яка в даному випадку, звичайно, дорівнює точці кипіння рідини при нормальному атмосферному тиску P. отже,

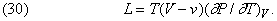
Це співвідношення було виведено шляхом аналізу теплового циклу, запропонованого французьким інженером Б.Клапейрон (1799-1864) в 1834. Воно показує, що теплоту пароутворення необов'язково визначати калориметричних методами; її можна обчислити по розширенню, що відбувається при випаровуванні, якщо відома швидкість підвищення тиску насиченої пари рідини при підвищенні температури, коли підтримується постійним обсяг системи. Це типове рівняння термодинаміки, що встановлює співвідношення між здавалося б не пов'язаними один з одним змінними.

Шляхом аналогічних міркувань Р.Клаузиус (1822-1888) вивів вираз для різниці теплоємностей Cs твердої і Cl рідкої фаз:

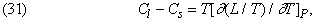
яке, втім, простіше вивести зі співвідношення (15).

Оскільки він розглядав рівняння Клапейрона і вніс, за його словами, «невеликі зміни» в хід міркувань, за співвідношенням (30) закріпилася назва рівняння Клаузіуса - Клапейрона.

Розмірковуючи в якійсь мірі аналогічно, можна, користуючись першим з співвідношень Максвелла, вивести формулу, яка показує вплив тиску на температуру плавлення твердої речовини, теплоізольованого так, що його ентропія постійна:

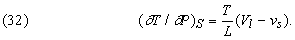
Тут L - теплота плавлення, T - температура плавлення при даному тиску P, а (Vl - vs) - зміна обсягу твердої речовини при плавленні. У разі льоду при плавленні відбувається стиснення, і формула (32) показує, що з підвищенням тиску температура плавлення знижується. Досвідчені дані узгоджуються з результатами обчислень. Більшість інших твердих речовин при плавленні розширюється, і, отже, їх температури плавлення підвищуються з підвищенням тиску.

Вплив тиску.

Інші ефекти, пов'язані з ізотермічним зміною тиску, описуються формулами

Ефект Джоуля - Томсона.

Якщо газ знаходиться в теплоизолированном посудині і над ним не здійснюється робота (H = const), то зміна його температури, обумовлене зміною тиску, дається формулою

Для ідеального газу aT = 1, і тому його температура не повинна змінюватися. Отже, зі зміни температури, виміряного, наприклад, при розширенні газу в вакуум, можна оцінювати ступінь відхилення реального газу від ідеального. Такий ефект дійсно спостерігається, і по імені вчених, які відкрили його, називається ефектом Джоуля - Томсона.

Вплив температури.

Точно так же виводяться формули, що описують вплив температури при постійному тиску:

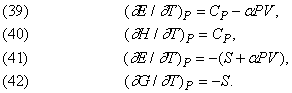
Інші співвідношення.

Різниця теплоемкостей при постійному тиску і при постійному обсязі дається виразом

Вираз для швидкості з звуку в газі має вигляд

де D - щільність газу, а g = CP / CV.

Багато що можна розраховувати графічними методами на основі експериментальних даних, не роблячи ніяких припущень про аналітичні співвідношення між величинами. Але в тих випадках, коли є алгебраїчні вирази, що описують розглядаються явища, остаточні результати часто вдається отримати простим диференціюванням і інтеграцією.

Наприклад, в діапазоні від абсолютного нуля до деякої граничної температури, для кожної речовини своєї, теплоємність всіх речовин при постійному обсязі пропорційна кубу температури (за шкалою Кельвіна):

Цей вислів вивів на основі квантової теорії П.Дебай (1884-1966). Воно дозволяє простим інтегруванням обчислювати повну ентропію при температурах, близьких до 0 К:

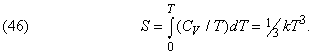
Рівняння стану.

Завдяки своїй простій формі газовий закон [формула (18)] дозволяє робити важливі висновки про властивості ідеального газу. Але при адіабатичному стисненні ідеальний газ нагрівається. В цьому випадку ізотермічний закон PV = NRT не виконується, і його необхідно замінити рівнянням

де g - відношення питомих теплоємностей при постійному тиску і при постійному обсязі, т. е. g = CP / CV. Це рівняння вивів французький математик С.Пуассон (1781-1840).

У робочих циліндрах теплових машин (парових машин, бензинових, газових і дизельних двигунів) швидкість стиснення велика, але процес не є повністю адиабатическим і називається Політропний. При вирішенні більшості проектно-конструкторських завдань в таких випадках приймається рівняння виду

де n - постійна величина, менша ніж g, і її перевищення над одиницею залежить від швидкості стиснення. Крім того, поведінка реальних газів відхиляється від рівнянь (18), (47) і (48), і для них використовуються т.зв. рівняння стану.

Прикладом таких рівнянь може служити

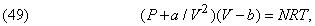
де a і b - константи, що залежать від природи газу. Це рівняння вивів Я.Ван-дер-Ваальса (1837-1923). Було запропоновано чимало і інших рівнянь; деякі з них справедливі тільки для одного газу.