Журнал РАДІОЛОЦМАН, серпень 2015
Володимир Рентюк, Запоріжжя, Україна
Частина 1
Для збільшення придушення використовують каскадне включення одиночних ланок. У професійній технічній літературі, наприклад, в [ 1 ] Говориться, що частота зрізу для випадку n ланок з однаковими частотами зрізу дорівнює
де
FCi - частота зрізу однієї ланки,
α - коефіцієнт, що визначається за формулою:
де n - кількість ланок в фільтрі.
Автор зустрічав в технічній літературі і інші «наближені» формули для розрахунку подібних структур, наприклад,
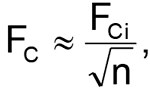
але всі вони дають велику похибку, і користуватися ними навіть для оціночних розрахунків не варто. Формула (4) хороша в теорії, але не на практиці. На рисунку 3 показані два, скоєно однакових з точки зору теорії ФНЧ.
Малюнок 3.Два варіанти триланкових ФНЧ на основі RC-ланок.
Як ми бачимо, представлена на рисунку 3 структура є багатоланковим фільтром, складеним з фільтрів першого порядку. Якщо вірити теорії, то загасання повинно бути 18 дБ / октава або 60 дБ / декада. Оскільки частоти зрізу всіх ланок рівні і становлять приблизно 1 кГц, то знову ж таки, відповідно до теорії, частота зрізу такого триланкового фільтра дорівнює 506 Гц, а переворот фази на 180 ° повинен відбуватися на частоті 1.7 кГц.
Насправді:
- для варіанту а) частота зрізу дорівнює приблизно 192 Гц,
- для варіанту б) частота зрізу дорівнює 455 Гц.
У частині ФЧХ і коефіцієнтів загасання ми маємо:
- для варіанту а) загасання 26 дБ / декада в першій декаді, переворот фази на 180 ° на 2.4 кГц;
- для варіанту б) загасання 40 дБ / декада в першій декаді, переворот фази на 180 ° на 1.8 кГц.
Як бачимо, перед нами два абсолютно різних фільтра (їх АЧХ показані на рисунку 4), і не один з них в повній мірі не відповідає класичній теорії. Автор цієї статті, будучи вже досить досвідченим інженером, допустив подібну грубу помилку при розробці фільтра для придушення частоти вибірки сигналу в багатоканальній системі зв'язку. Таким чином, при побудові багатоланкових ФНЧ вибір номіналів елементів для їх реалізації необхідно наближати до виду, наведеним на рисунку 3б, або розділяти ланки буферними підсилювачами, що зводить нанівець ряд переваг цих фільтрів: збільшує рівень шумів, зменшує динамічний діапазон, збільшує нелінійні спотворення. Крім того, повторюся, тут для спрощення було розглянуто ідеальний варіант використання фільтра, коли вихідний опір джерела сигналу дорівнює нулю, а опір навантаження фільтра - нескінченності. Отже, необхідно враховувати, як це було показано вище для одноланкового фільтра, і реальні умови використання фільтра.
Якщо розглядати окремі ФНЧ як неминучі частини якоїсь загальної схеми, то ми можемо побачити, що вони можуть бути утворені лініями передачі сигналу, підсилювальними каскадами (всі вони мають обмежену смугу пропускання в області високих частот), вихідним опором і ємністю навантаження. Всі ці лінійні спотворення в комплексі складно піддаються аналізу і вимагають ретельного моделювання.
А яким може і повинен бути підхід до фільтрів високої частоти? Тут найбільш типовий випадок - багатоланкові ФВЧ, але не як окрема структура, типу представленої на рисунку 3, а у вигляді декількох каскадів з розділовими конденсаторами. Такі каскади можна і потрібно вважати еквівалентними ФВЧ першого порядку (Малюнок 2а). Якщо для випадку з ФНЧ, як це зазначено вище, провести оцінку досить складно, то для окремих елементарних ФВЧ їх сумарну АЧХ відносно легко оцінити за формулами.
Модуль передавальної функції фільтра описується таким же виразом, як і для ФНЧ:
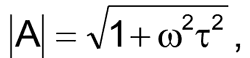
де:
ω - циклічна частота, рівна 2πf,
τ - постійна часу, що дорівнює в нашому випадку RC.
Тут, для більшості випадків:
R - вхідний опір,
С - ємність розділового конденсатора.
Оскільки модуль передавальної функції аналогічний ФНЧ, то і частота зрізу визначається аналогічно, як
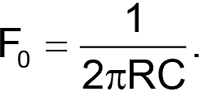
А ось ФЧХ фільтра має відміну від ФНЧ:
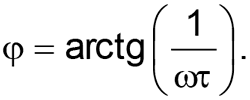
Як правило, вихідний опір джерела сигналу значно менше опору навантаження, тому наведені формули можуть використовуватися на практиці без особливих обмежень. Якщо ж ця умова не дотримується, той в формулах необхідно враховувати сумарний опір.
Для випадку послідовного з'єднання ФВЧ результуюча частота зрізу може бути легко визначена за наближеною формулою:
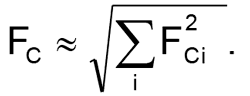
Тут таке наближення доречно для практики і не дає великий похибки. Вищевикладене стосувалося виключно фільтрів. Але, як було вже сказано, всі, що б ми не проектували, в результаті виявляється певним фільтром, тобто підсилювальний тракт апріорі матиме певний рівень лінійних спотворень. Тому на практиці нам часто буває необхідно розподілити допустимі лінійні спотворення між каскадами. Причому, краще зробити це все заздалегідь, щоб не опинитися в ситуації персонажа з відомого анекдоту ( «Ах, якби я був такий розумний зараз, як моя дружина потім!»). Повірте, краще все, що можна, заздалегідь розрахувати і оцінити, ніж сидіти потім з паяльником, підбираючи елементи і використовуючи при цьому відомі ідіоматичні вирази.
Щоб уникнути подібної ситуації, необхідно привести еквівалентну схему тракту до системи елементарних лінійних фільтрів першого порядку і розподілити між ними допустимі лінійні спотворення. У визначенні елементів елементарного ланки вам допоможе формула, виведена автором статті ще на початку його кар'єри інженера. За основу береться відоме еквівалентний опір R елементарної комірки, наприклад, це може бути вхідний опір каскаду (для випадку з ФВЧ), опір джерела сигналу або вихідний опір каскаду (для випадку з ФНЧ). Для кожної елементарної комірки на заданій частоті F закладається максимально допустимий рівень лінійних спотворень N (в децибелах) і розраховується максимально (для випадку ФНЧ) або мінімально (для випадку з ФВЧ) допустима для цих умов ємність конденсатора C. Для випадку з ФНЧ цей конденсатор буде ємнісний частиною навантаження, а для випадку з ФВЧ - розділовим. Формули для розрахунку мають вигляд:
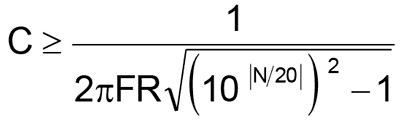
для ФВЧ і
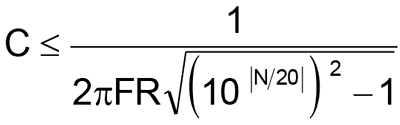
для ФНЧ.
При необхідності їх можна легко вирішити щодо R або F.
Якщо перейти до змішаних структурам, то одним з найпоширеніших і цікавих з практичної точки зору варіантів є частотно компенсований дільник напруги, нерідко має ємнісне навантаження. Наприклад, він може бути навантажений на лінію передачі, а звичайний екранований кабель має типову погонну ємність 100 пФ / м, про що розробники часто забувають. У загальному вигляді така система має вигляд, представлений на рисунку 5.
Чи не завантажуючи читачів обчисленнями, відразу дамо практичну формулу. Для повної компенсації ємності навантаження необхідно виконати умову C1 / C2 = R2 / R1. Перевірка правильності вибору компенсує ємності С1 здійснюється подачею на вхід дільника імпульсу напруги і оцінкою його спотворень. Правильно підібрана частотна компенсація на коефіцієнт передачі подільника впливу не робить.
Поєднавши однозвенной ФНЧ і ФВЧ, ми отримаємо примітивний смуговий фільтр (ППФ), зображений на рисунку 6.
У загальному вигляді саме до такого фільтру можуть бути приведені еквівалентні схеми більшості підсилювачів. ФВЧ утворений елементами C1 і R2, а ФНЧ - елементами R1 і C2. Відповідно, він може бути легко розрахований з урахуванням наведених вище формул і уточнень.
Центральна частота фільтра буде збігатися з частотами зрізу утворюють його ФВЧ і ФНЧ, і дорівнює
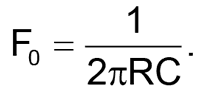
Фаза фільтра буде змінюватися від + 90 ° до -90 °, а фазовий зсув на центральній частоті буде дорівнює нулю.
Формули для практичного розрахунку наступні:
для варіанту а)
R2 = R,
C2 = C,
R1 = mR2,
C2 = C / m, 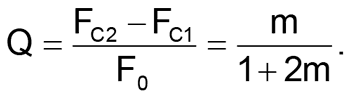
для варіанту б)
R2 = R,
C2 = C,
R1 = mR2,
C2 = C / m, 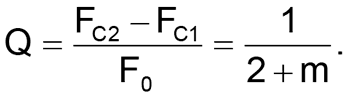
Тут FC2 і FC1 - верхня і нижня частоти зрізу фільтра, відповідно.
Ця структура може використовуватися і в якості селективного фільтра з максимальною добротністю Q = 0.5; в цьому випадку R1 = R2 = R, а C1 = C2 = C. Коефіцієнт передачі на частоті резонансу буде дорівнює 1/3, а частота резонансу буде дорівнює центральній частоті F0.
Якщо цей фільтр доповнити дільником напруги з коефіцієнтом передачі 1/3, а сигнал зняти з діагоналі отриманого моста, то ми прийдемо до відомою схемою моста Вина-Робертсона. Ця схема є вже режекторний фільтр, а вірніше, фільтром з придушенням частоти резонансу. Його ФЧХ на частоті резонансу матиме стрибок з -90 ° до + 90 °. В якості фільтра така структура використовується вкрай рідко, вона знайшла своє застосування в генераторах синусоїдальних коливань.
Найбільш часто для придушення небажаної частоти використовується інший варіант комбінованого фільтра, а саме, зображений на рисунку 7, подвійний Т-подібний.
Незважаючи на низьку, характерну для всіх RC-фільтрів, добротність, даний Т-міст може придушити сигнал з частотою свого резонансу, по крайней мере, на 50 дБ (Малюнок 8). Частота резонансу збалансованого моста (Малюнок 7) визначається за формулою
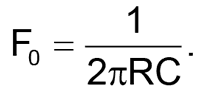
При необхідності знизити рівень придушення паралельно мосту включається додатковий резистор. Найчастіше така схема використовується в ланцюзі негативного зворотного зв'язку. В цьому випадку вона стає не переважної, а селективної. Аналогічні фільтри використовувалися в приставках «вау-вау» для електрогітар.
Подібні схеми автор використовував в складі кінцевих ступенів формування тембру в своїх ЕМІ серії «СИМОНА» і синтезаторі «Аля» [ 3 ]. На основі Т-моста був виконаний регульований формантний фільтр [ 2 ]. Використання такого простого рішення допоможе вам збагатити і прикрасити звучання, наприклад, генератора музичних сигналів, звучання якого в звичайному виконанні є простою, вибачте, «пілікалкой», або зажадає складних програмних рішень. (Тембр, отриманий за допомогою такого фільтра, можна прослухати, скачавши з [ 3 ] Семпли ДКЕМІ «СИМОНА»).
На завершення на рисунку 9, виключно як приклад використання складних фільтрових комбінацій на основі RC-ланцюгів, наведена схема трьохсмугового регулятора тембру, який був розроблений автором статті в 1983 році для першого в СРСР моноблочного музичного центру вищого класу «Такт-011 стерео».
У наступній статті, присвяченій цій темі, будуть розглянуті практичні питання проектування LC- і RLC-фільтрів.
література
- Титце У., Шенк К. Напівпровідникова схемотехніка. 12-е изд. Том 1, 2: Пер. з нім. - М .: ДМК Пресс, 2008.
- Рентюк В. «Синтез музичних тембрів», цикл статей, Радіоаматор, №10, 11 2011, №1, 3, 4 2012.
- Музей радянських синтезаторів

