ЧИ АЛГЕБРА - векторний простір , На к-ром визначена операція, яка називається коммутирования. Для елементів алгебри визначені лінійні операції - додавання і множення на число. Якщо допускається множення на дійсні числа, то Л. а. наз. речової; якщо допускається множення на комплексні числа, то Л. а. наз. комплексною. Операція коммутирования зіставляє будь-яким двом елементам алгебри X,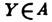 
третій елемент 
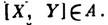Ця операція білінійну (т. Е. Лінійна по кожному аргументу), антисиметрична 
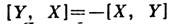і задовольняє тотожності Якобі
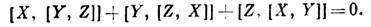
Поняття "Л. а." виникло в зв'язку з вивченням груп Лі, т. к. елементи групи Лі можна представляти у вигляді експонент від елементів Л. а. (Див. Група ) .Якщо група Лі реалізована як група матриць, то відповідна їй Л. а. також є матричної. Це означає, що кожен елемент алгебри є матрицею, а операція коммутирования визначається як звичайний комутатор: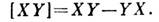 
Основні поняття. Якщо у векторному просторі А обраний базис Х1. . ., Xn (т. Е. Повний набір лінійно незалежних елементів), то для визначення на А структури Л. а. досить задати попарні комутатори базисних елементів, т. е. коеф.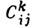 
в ф-ле 
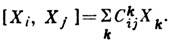Тоді комутатори довільних елементів простору А однозначно визначаються тим, що кожен такий елемент можна представити у вигляді лінійної комбінації базисних елементів 
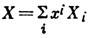і що операція коммутирования є билинейной. Коеф. 
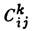наз. структурними константами даної Л. а. Вони залежать від вибору базису, але при будь-якому виборі є антисиметричного по нижнім індексами і задовольняють умові
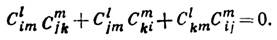
Гомоморфизмом або представлений і-е м алгебри Лі А 1 в алгебру Лі А 2 зв. таке лінійне відображення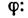 
(Т. Е. Відображення, що зберігає лінійні операції), до-рої погоджено з операціями коммутирования в обох алгебрах: 
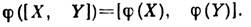Ядром гомоморфізму зв. підмножина в алгебрі A 1, к-рої під дією j переходить в нульовий елемент алгебри А 2. Якщо відображення 
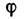взаємно однозначно, то воно наз. изоморфизмом або точним поданням. В цьому випадку ядро відображення дорівнює нулю. Будь-яка скінченновимірна Л. а. допускає точне уявлення в алгебру матриць (теорема А д о). З огляду на тісний зв'язок, що існує між Л. а. і групами Лі, завдання вивчення уявлень груп Лі у великій мірі зводиться до вивчення уявлень Л. а. Саме цим пояснюється прикладне значення теорії Л. а. і їх уявлень (див. подання групи ).
Якщо ввести в розгляд матриці Сi з матричними елементами, рівними структурним констант,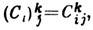 
то умова на структурні константи, наведене вище, можна переписати у вигляді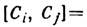 
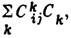де дужки позначають звичайний комутатор двох матриць. Т. о., Матриці С i здійснюють n -мірним уявлення базисних елементів Xi, а їх лінійні комбінації - уявлення всієї Л. а. Це т. Зв. приєднане уявлення adX. Сукупність елементів, комутуючих з усіма елементами алгебри, наз. центром Л.а.
підмножина 
в Л. а. наз. подалгебру Лі, якщо вона сама є Л. а. щодо тих же операцій. Це означає, що В - лінійне підпростір, і операція коммутирования не виводить з В. Останнє можна записати символічно: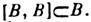 
Якщо для підпростору 
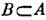виконується більш сильне умова 
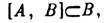то В зв. ідеалом в А. Якщо В - ідеал, то фактор-простір А / В, елементами догрого є класи Х + У (т. Е. Безлічі елементів виду X + Y, де У пробігає все В), саме є Л. а. Операції в цій фактор-алгебри визначаються природ. чином, т. е. з допомогою операцій, здійснених над будь-якими представниками класів, напр.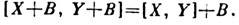 
Будь-яка Л. а. містить тривіальні (невласні) ідеали. Один з них збігається з усією Л. а., Другий складається лише з нульового елемента. Якщо Л. а. не містить ідеалів, відмінних від цих (т. е. не містить власної. ідеалів), то вона ІАЗ. простий. Алгебра зв. полуприем, якщо вона не має нетривіальних комутативний ідеалів (т. е. таких, в яких брало все комутатори звертаються в нуль). Будь-яка полуприем Л. а. представляється у вигляді прямої суми простих Л. а.
Л. а. А зв. можливо розв'язати, якщо в ній існує такий ланцюжок подалгебр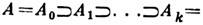 
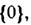що А i + 1-ідеал в А; і фактор-алгебра A i / Ai + 1 коммутативна. Якщо, крім того, всі A i - ідеали в А і фактор-алгебра Ai / Ai + 1 належить центру фактор-алгебри A / Ai + 1, то алгебра А наз. нильпотентною.
На Л. а. можна ввести внутр. твір, визначивши його рівністю (X, Y) = Тr (аd Х * ad Y), де Тr означає слід оператора (матриці). Ця симетрична (щодо перестановки аргументів) билинейная форма зв. формою Кіллінг. Якщо скористатися матричної реалізацією приєднаного уявлення, можна висловити форму Кіллінг через коеф. хi, уi розкладання елементів X, Y по базису. отримаємо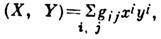 
де симетричний тензор 
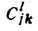наз. метричним тензором Картана алгебри А. Для деяких Л. а. метрич. тензор і форма Кіллінг можуть бути виродилися, т. е. det 
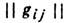= 0 (це має місце, напр., Для комутативний л. А.). Форма Кіллінг невирождени тільки для полуприем Л. а. (Критерій Картана).
Для комплексних простих Л. а. завжди можна вибрати базисні елементи Xi - таким чином, щоб структурні константи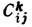 
були чисто уявними і антисиметричного по всім парам індексів. Такий набір зв. базисом Картана. При цьому ранг алгебри Л і l визначається як макс. число комутуючих елементів в базисі Картана, l -мірним комутативна подалгебра, натягнута на це безліч елементів, зв. подалгебру Картана,
Класифікація алгебр Лі. Є чотири серії простих комплексних Л. а. кінцевої розмірності: Al, Bl, Сl, Dl і крім цього п'ять виняткових алгебр G 2, F4, Е6, E 7, E 8 (індекси всюди позначають ранг алгебри). Кожна комплексна Л. а. має єдину речову подалгебру, що є Л. а. компактної групи Лі. Перерахуємо компактні групи, відповідні серіям. Алгебра Аl, l = 1, 2,. . . , Має розмірність n = (l + l) 2-1 і пов'язана з групою SU (l + 1) унітарних унімодулярних (т. Е. Мають одиничний детермінант) (l +1) -рядних матриць. Алгебра Bl, l = 2, 3,. . ., Має розмірність n = = l (2 l +1) і пов'язана з групою SO (2 l +1) ортогональних унімодулярних матриць порядку 2l + 1. Випадок l = l виключається, т. К. В1 = А1. Алгебра Сг, 1 = 3, 4,. . ., Має розмірність n = l (2l + 1) а пов'язана з сімплектіческой групою Sp (21) (т. Е. Групою перетворень, що зберігають невироджених антисиметричного білінійну форму в просторі розмірності 21). При l = 1 і 2 має місце збіг Cl = Bl. Алгебра Dl, l = 4, 5,. . ., Має розмірність n = 2 l 2l і пов'язана з групою SO (2l). Нижчі розмірності виключаються, т. К. D3 = A3, a D1 і D 2 не є простими. Групи SU (n), SO (n), Sp (n), що породжуються нескінченними серіями Л. а., Наз. класичними групами.
Кожна комплексна проста Л. а. має неск: речових форм (т. е. таких речових Л. а., з яких брало дана Л. а. виходить комплексіфікаціей). Лише одна з них відповідає компактною групі Лі. Решта призводять до некомпактних груп. Напр., Серед речових форм комплексної алгебри Al є такі, к-які відповідають групам SU (p, q), p + q = l + 1, псевдоунітарних матриць, т. Е. Перетворень в. комплексному (l + 1) -мірному просторі. зберігають форму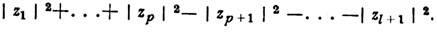 
Речові форми алгебри Bl породжують групи псевдовращеній або псевдоортогональних перетворень SO (p, q), p + g = 2 l + l. Це перетворення узагальненого простору Маньківського з р просторовими і q тимчасовими вимірами. Речові форми в Cl породжують групи Sp (2p, 2q), p + q = l. Таку групу можна визначити як підгрупу в групі SU (2p, 2q), що залишає інваріантної антисиметричного білінійну форму. Ще одна матеріальна форма в Сl складається з антіермітових матриць і породжує групу 
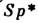(2 l). Речові форми в Dl породжують групи псевдовращеній SO (p, q), p + q = 2l.
Крім перерахованих, є недо-які спеціальні речові форми комплексних алгебри Аl і Dl. Наведений список не повний з точки зору класифікації простих груп. Не кожна проста матеріальна група Лі є речовій формою простий комплексної групи. Так, алгебра Dl на проста, і не проста відповідна їй компактна підгрупа SO (4). Однак некомпактності група SO (1, 3) ( Лоренца група ) Є простою. Її Л. а. ізоморфна sl (2, С). Узагальненням цього прикладу є цілий клас простих речових Л. а.- це комплексні Л. а., Що розглядаються як речові.
Літ .: Джекобсон Н., Алгебри Лі, пров. з англ., М., 1964; Дубровін Б. А., Новиков С. П., Фоменко А. Т., Сучасна геометрія, 2 вид., М., 1986.
А. А. Кирилов, М. Б. Менський.
покажчик >>
